引言
近来,在开展课题时遇到了需要将梯形波进行傅里叶级数展开的问题,查询了一些资料(惭愧,一开始就没想着自己动手积分),然后没有找到自己想要的结果(其实有相近的,只不过不是任意周期的,当时没有转变过来),最后还是动手算出来了,在这里做一个小小的记录,算是回顾以前的知识吧,捂脸。
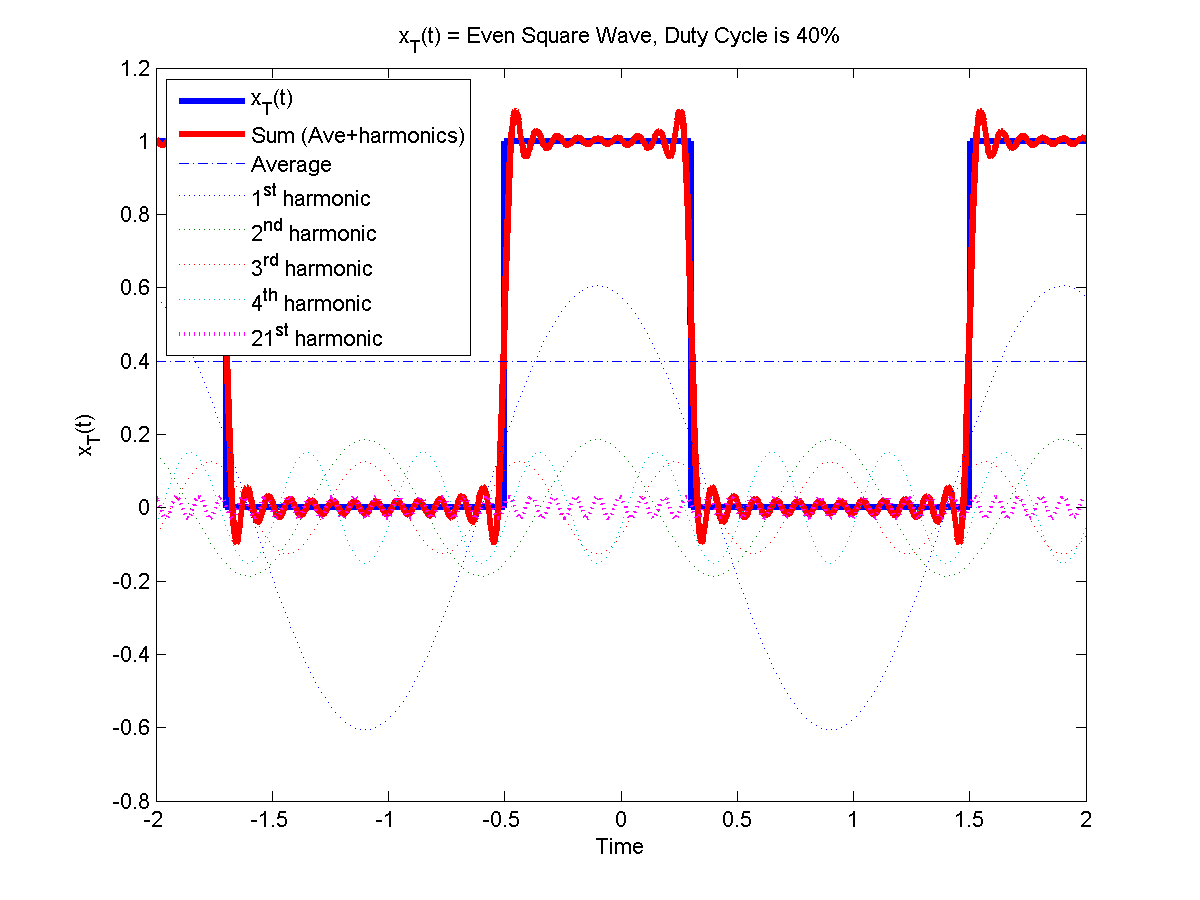
由于像三角波,矩形波,梯形波这种波形不连续,因此在仿真软件中很容易出现计算不收敛的情况。所以,在这种情况下,利用一系列谐波叠加的形式来等价于原来的波形,可以很好的优化模型。
预备知识
公式
给定一个周期为 \(T\) 的函数 \(x(t)\) ,那么它可以表示为无穷级数:
\[ f(x) \sim \frac{a_0}{2} + \sum_{n=1}^{\infty} \left [a_n \cos \left (\frac{2 {\pi} nx}{T} \right ) + b_n \sin \left (\frac{2 {\pi} nx}{T} \right ) \right ] = \sum_{n=-\infty}^{\infty} c_n e^{i \frac{2 {\pi} nx}{T} } \]
其中傅里叶系数为:
\[ \left \{ \begin{aligned} a_n = &\frac{2}{T} \int_{t_0}^{t_0+T} f(t) \cdot \cos \left (\frac{2 {\pi} nt}{T} \right )dt \qquad &n=0, 1, 2, \cdots \\[2ex] b_n = &\frac{2}{T} \int_{t_0}^{t_0+T} f(t) \cdot \sin \left (\frac{2 {\pi} nt}{T} \right )dt &n=1, 2,3, \cdots \\[2ex] c_n = &\frac{1}{T} \int_{t_0}^{t_0+T} f(t) \cdot e^{-i \frac{2 {\pi} nt}{T} }dt &n=0, \pm 1, \pm 2, \cdots \end{aligned} \right. \]
性质
- 收敛性
在闭区间上满足狄利克雷条件的函数表示成的傅里叶级数都收敛。狄利克雷条件如下:
- 在定义区间上,\(x(t)\)需绝对可积;
- 在任一有限区间中,\(x(t)\)只能取有限个极值点;
- 在任何有限区间上,\(x(t)\)只能有有限个第一类间断点。
满足上述条件的\(x(t)\)傅里叶级数都收敛,且:
- 当\(t\)是\(x(t)\)的连续点时,级数收敛于\(x(t)\)
- 当\(t\)是\(x(t)\)的间断点时,级数收敛于\(\frac{1}{2} \left [x(t^-)+x(t^+) \right ]\)
- 正交性
所谓的两个不同向量正交是指它们的内积为0,这也就意味着这两个向量之间没有任何相关性,例如,在三维欧式空间中,互相垂直的向量之间是正交的。三角函数族的正交性用公式表示出来就是:
\[ \left\{ \begin{aligned} &\int_0^{2 \pi} \cos(mx) \cdot \cos(nx) dx =0 \qquad (m \ne n) \\[2ex] &\int_0^{2 \pi} \sin(nx) \cdot \sin(nx) dx = \pi \\[2ex] &\int_0^{2 \pi} \cos(nx) \cdot \cos(nx) dx = \pi \end{aligned} \right. \]
- 奇偶性
奇函数\(f_o(x)\)可以表示为正弦级数,而偶函数\(f_e(x)\)则可以表示成余弦级数:
\[ \begin{aligned} f_o(x) &\sim \sum_{n=1}^{\infty} b_n \sin \left (\frac{2 {\pi} nx}{T} \right ) \\ f_e(x) &\sim \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos \left (\frac{2 {\pi} nx}{T} \right )\end{aligned} \]
几种常见波形的傅里叶级数展开式
梯形波(奇函数)
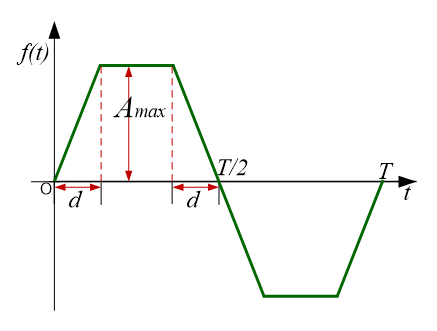
如上图所示,该梯形波是一个周期为T的奇函数,幅值为\(A_{max}\),上升沿时间为\(d\),在区间\(\left [0, \frac{T}{2} \right ]\)的函数表达式为:
\[ f(t) = \begin{cases} \frac {A_{max} }{d} t, \qquad \qquad & 0 \le t \le d \\[2ex] A_{max}, & d \le t \le \frac{T}{2} - d \\[2ex] \frac {A_{max} }{d} \left (\frac{T}{2} - t \right ), & \frac{T}{2} - d \le t \le \frac{T}{2} \end{cases} \]
由奇偶性可知,该波形在区间\(\left [-\frac{T}{2}, \frac{T}{2} \right ]\)的傅里叶级数展开式为:
\[ f(t) \sim \sum_{n=1}^{\infty} b_n \sin \left (\frac{2 {\pi} nt}{T} \right ) \]
其中傅里叶系数为:
\[ b_n = \frac{2}{T} \int_{-\frac{T}{2} }^{\frac{T}{2} } f(t) \cdot \sin \left (\frac{2 {\pi} nt}{T} \right )dt \quad \quad n=1, 2,3, \cdots \]
将\(f(t)\)函数代入傅里叶系数表达式中,可得:
\[ \begin{aligned} b_n &= \frac{2}{T} \int_{-\frac{T}{2} }^{\frac{T}{2} } f(t) \cdot \sin \left (\frac{2 {\pi} nt}{T} \right )dt = \frac{4}{T} \int_{0}^{\frac{T}{2} } f(t) \cdot \sin \left (\frac{2 {\pi} nt}{T} \right )dt \\[2ex] &= \frac{4}{T} \left [ \int_0^d \frac{A_{max} }{d} t \cdot \sin \left (\frac{2 {\pi} nt}{T} \right )dt + \int_d^{\frac{T}{2} - d} A_{max} \cdot \sin \left (\frac{2 {\pi} nt}{T} \right )dt + \int_{\frac{T}{2} - d}^{\frac{T}{2} } \frac{A_{max} }{d} \left (\frac{T}{2}-t \right ) \cdot \sin \left (\frac{2 {\pi} nt}{T} \right )dt \right ] \\[2ex] &= \left . \left . \frac{4}{T} \left [ -\frac{A_{max} }{d} {T \over {2 \pi n} } \cdot t \cdot \cos \left ( \frac{2\pi nt}{T} \right ) \right | _0^d + {A_{max} \over d } {T^2 \over 4 \pi^2 n^2} \cdot \sin \left( {2 \pi n t \over T} \right ) \right | _0^d \right ] + {4 \over T} \left [ \left . - {A_{max}T \over 2 \pi n} \cdot \cos \left( {2\pi nt \over T}\right) \right |_d^{ {T \over 2}-d} \right ] + {} \\[2ex] &{} + \left. {4 \over T} \left [ -{A_{max} \over d} {T \over 2 \pi n} \cdot \left ( {T \over 2} - t \right ) \cdot \cos \left ( \frac{2\pi nt}{T} \right ) \right | _{ {T \over 2} - d}^{T \over 2} - \left . {A_{max} \over d}{T^2 \over 4 \pi^2 n^2} \cdot \sin \left( {2 \pi n t \over T} \right ) \right | _{ {T \over 2} - d}^{T \over 2} \right ] \\[2ex] &= {4 \over T} \left \{ {A_{max} T^2 \over 4d \pi ^2 n^2} \left [ \sin \left( {2 \pi n \over T} \cdot d \right) + \sin \left( {2 \pi n \over T} \cdot \left( {T \over 2} - d \right ) \right) \right ] \right \} ={A_{max} T \over d \pi ^2 n^2} \left[ \sin\left( {2 \pi n d \over T} \right) + \sin \left( n\pi - {2 \pi n d \over T} \right) \right] \end{aligned} \]
由 \[ \sin \left( n\pi - {2 \pi n d \over T} \right) = \begin{cases} \sin\left( {2 \pi n d \over T} \right) \qquad \qquad &n=2N-1 \\[2ex] -\sin\left( {2 \pi n d \over T} \right) &n=2N \end{cases} \] 可得:
\[ b_n = \begin{cases} {2 A_{max} T \over d \pi ^2 n^2} \left[ \sin\left( {2 \pi n d \over T} \right) \right ] \qquad \qquad &n=2N-1 \\[2ex] 0 &n=2N \end{cases} \]
综上所述,可以得到该梯形波在区间\(\left[ -{T \over 2}, {T \over 2} \right ]\)的傅里叶级数展开式为:
\[ f(t) \sim {4 A_{max} \over \pi \omega d} \sum _{n=1}^{\infty} {\sin ( { (2n-1) \omega d }) \over (2n-1)^2} \cdot \sin((2n-1) \omega t) \qquad n=1,2,3,\cdots \] 其中:\(\omega = {2 \pi \over T}\)
脉冲波(偶函数)
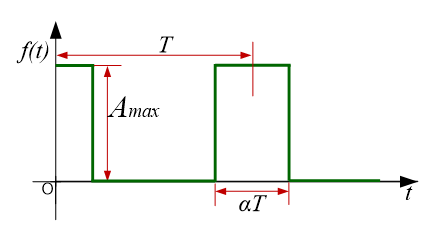
如上图所示,该脉冲波是一个周期为T的偶函数,幅值为\(A_{max}\),脉冲宽度为\(\alpha T\),在区间\(\left[ -{T \over 2}, {T \over 2} \right ]\)的函数表达式为:
\[ f(t)= \begin{cases} A_{max}, \quad &|t| \le { {\alpha T} \over 2} \\[2ex] 0, &|t| \gt { { {\alpha T} } \over 2} \end{cases}, \qquad - {T \over 2} \le t \le {T \over 2} \]
由奇偶性可知,该波形在区间\(\left[ -{T \over 2}, {T \over 2} \right ]\)的傅里叶级数展开式为:
\[ f(t) \sim \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos \left (\frac{2 {\pi} n t}{T} \right ) \]
其中傅里叶系数为:
\[ a_n =\left\{\begin{aligned} &{2 \over T} \int_{-{T \over 2} }^{T \over 2} f(t) dt \qquad \qquad \qquad \qquad & n=0 \\[2ex] &\frac{2}{T} \int_{-\frac{T}{2} }^{\frac{T}{2} } f(t) \cdot \cos \left (\frac{2 {\pi} nt}{T} \right )dt & n=1, 2,3, \cdots \end{aligned}\right. \]
将\(f(t)\)函数代入傅里叶系数表达式中,可得:
\[ \begin{aligned} a_0 &= {2 \alpha A_{max} } \\[2ex] a_n &={2 \over T} \int _{-{\alpha T \over 2} }^{\alpha T \over 2} A_{max} \cos \left (\frac{2 {\pi} nt}{T} \right )dt = {4 \over T} \int _{0}^{\alpha T \over 2} A_{max} \cos \left (\frac{2 {\pi} nt}{T} \right )dt\\[2ex] &= \left . {4 \over T} {A_{max} T \over 2 \pi n } \sin \left( {2 \pi n t \over T} \right) \right|_0^{\alpha T \over 2} ={2A_{max} \over n \pi} \sin (\alpha n \pi) \qquad \qquad \qquad \qquad n=1,2,3,\cdots \end{aligned} \]
因此,可以得到该梯形波在区间\(\left [ -{T \over 2}, {T \over 2} \right ]\)的傅里叶级数展开式为:
\[ f(t) \sim \alpha A_{max} + {2A_{max} \over \pi} \sum _{n=1}^{\infty}{\sin (\alpha n \pi) \over n} \cos(n\omega t) \qquad n=1,2,3, \cdots \]
其中:\(\omega = {2 \pi \over T}\)
方波(奇函数)
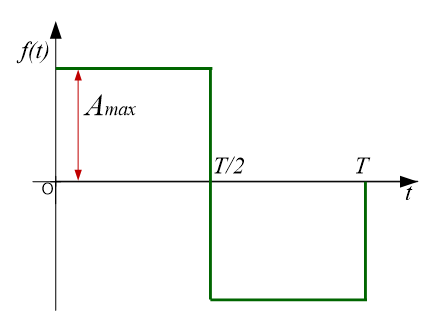
同理,该方波在区间\(\left [ -{T \over 2}, {T \over 2} \right ]\)的傅里叶级数展开式为:
\[ f(t) \sim {4A_{max} \over \pi} \sum_{n=1}^{\infty}{\sin((2n-1)\omega t) \over 2n-1} \qquad \qquad n=1,2,3,\cdots \]
其中:\(\omega = {2 \pi \over T}\)
三角波(奇函数)
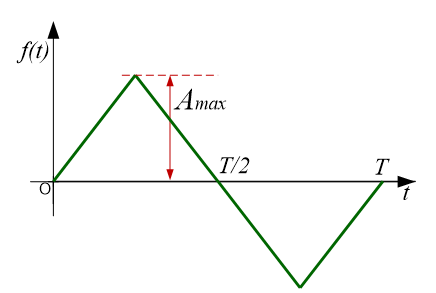
同理,该三角波在区间\(\left [ -{T \over 2}, {T \over 2} \right ]\)的傅里叶级数展开式为:
\[ f(t) \sim {8A_{max} \over \pi^2}\sum_{n=1}^{\infty}{(-1)^{n-1}\sin((2n-1)\omega t) \over (2n-1)^2} \qquad n=1,2,3,\cdots \]
锯齿波(非奇非偶函数)
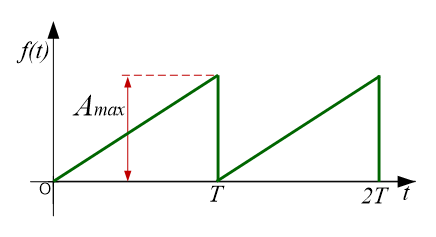
该锯齿波如上图所示,在区间\([0, T]\)的函数表达式为:
\[ f(t)={A_{max} \over T}t \qquad \qquad 0 \le t \le T \]
由于该函数为非奇非偶函数,因此,该波形在区间\([0, T]\)的傅里叶级数展开式为:
\[ f(x) \sim \frac{a_0}{2} + \sum_{n=1}^{\infty} \left [a_n \cos \left (\frac{2 {\pi} nx}{T} \right ) + b_n \sin \left (\frac{2 {\pi} nx}{T} \right ) \right ] \]
其中傅里叶系数为:
\[ \begin{aligned} a_n &= \frac{2}{T} \int_{0}^{T} f(t) \cdot \cos \left (\frac{2 {\pi} nt}{T} \right )dt \qquad \qquad & n=0, 1, 2, \cdots \\[2ex] b_n &= \frac{2}{T} \int_{0}^{T} f(t) \cdot \sin \left (\frac{2 {\pi} nt}{T} \right )dt & n=1, 2,3, \cdots \end{aligned} \]
将\(f(t)\)函数代入傅里叶系数表达式中,可得:
\[ \begin{aligned} a_0 &=A_{max} \\[2ex] a_n &= {2 \over T} \int_0^T{A_{max} \over T}t \cdot \cos \left( {2 \pi nt\over T} \right) dt \\[2ex] & = {2 \over T} {A_{max} \over T}{T \over 2 \pi n} \left . \left . \left[ t\sin \left({2\pi nt \over T}\right) \right| _0^T + {T \over 2 \pi n} \cos \left({2\pi nt \over T}\right) \right| _0^T \right] =0 \qquad &n=1,2,3,\cdots\\[2ex] b_n &= {2 \over T} \int_0^T{A_{max} \over T}t \cdot \sin \left( {2 \pi nt\over T} \right) dt \\[2ex] &= -{2 \over T} {A_{max} \over T}{T \over 2 \pi n} \left . \left . \left[ t\cos \left({2\pi nt \over T}\right) \right| _0^T - {T \over 2 \pi n}\sin \left({2\pi nt \over T}\right) \right| _0^T \right] =-{A_{max} \over n\pi} &n=1,2,3,\cdots \end{aligned} \]
因此,可以得到该锯齿波在区间\([0,T]\)的傅里叶级数展开式为:
\[ f(t) \sim {A_{max} \over 2}-{A_{max} \over \pi} \sum_{n=1}^{\infty} {\sin(n \omega t) \over n} \qquad \qquad n=1,2,3,\cdots \]
结语
这里仅仅列出了极小部分的波形的傅里叶级数展开式,对于其它波形,类似代入计算即可,给出公式之后,更多的是考验数学积分计算了。
参考文献
[1] 维基百科编者. 傅里叶级数
[2] 百度百科编者. 傅里叶级数